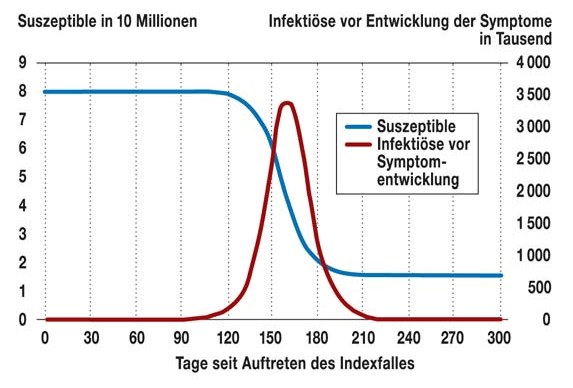
Im Deutschen Ärzteblatt vom 2009 fand ich die Modellierung einer ganz normalen und gewohnten Grippewelle, wie sie in dieser oder ähnlicher Form zur Grundausbildung aller Ärzte in den ersten Semestern gehört. Nicht alle Grippen sind gleich, aber das folgende bildet einen für Deutschland typischen Verlauf ab:
|
|
| Abb. 1: Verlauf einer normalen deutschen Grippewelle vom Tag des Auftretens der ersten Fälle an. (Mikolajczyk 2009) |
|
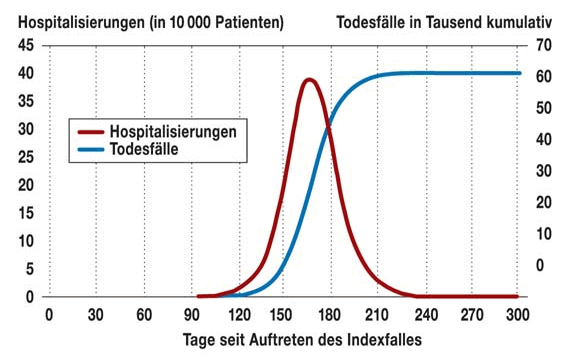
| Abb. 2: Auswirkungen und Folgen einer normalen deutschen Grippewelle. (Mikolajczyk 2009) |
Nichts, was über die derzeitige Welle von Covid-19 für Deutschland bekannt wurde, weicht substantiell vom oben gezeigten Verlauf ab. Wir wären demnach derzeit etwa am Tag 60 der beiden gezeigten Verläufe, mit einer Extrapolation der heutigen Steigerungsraten vielleicht auch kurz vor dem Tag 90.
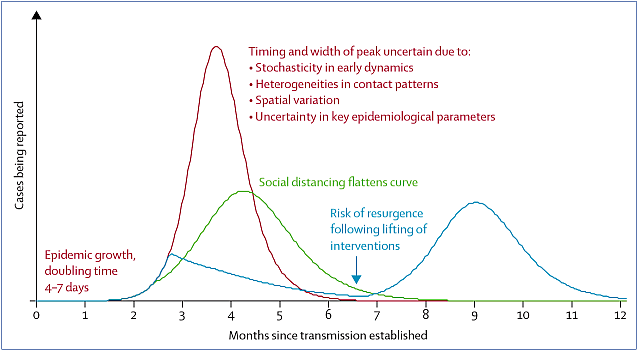
Sämtliche Quellen zu möglichen Eingriffen und Maßnahmen sind sich einig darüber, daß sie ausnahmslos an der Gesamtzahl der Fälle nichts ändern können. Sie können allenfalls den Verlauf etwas verlangsamen. Das ist sinnvoll und notwendig, um die Spitze der Welle abzuflachen und eine Überlastung der Gesundheitssysteme zu vermeiden. Wie das aussehen könnte, zeigt ein aktueller Artikel im Lancet:
|
| Abb. 3: Möglicher Einfluß restriktiver Maßnahmen und Einschränkungen auf den Verlauf einer Krankheitswelle. (Anderson 2020) |
Schulschließungen und Veranstaltungsverbote können nach den Erfahrungen der Vergangenheit durchaus wirksam sein und eine Welle spürbar abschwächen. Dazu müssen diese Eingriffe aber zum richtigen Zeitpunkt erfolgen und das Wirtschaftsleben wie die Infrastruktur müssen in einem stabilen Zustand sein, der es erlaubt, sie durchzustehen. Das bedeutet, sie müssen, wie in Abbildung 3 gezeigt, dann einsetzen, wenn der Anstieg der Welle sich deutlich abzeichnet. Für Deutschland bedeutet das um die 500 000 Fälle, etwa fünf Verdoppelungen oder mindestens 15 Tage von den heute bekannten 10 000 entfernt.
Das weiß derzeit niemand genau, denn so etwas Unsinniges ist den Vergangenheit bisher nie versucht worden. Wir stehen derzeit am Tag 60 der Abbildungen 1 und 2 oder etwas dahinter mit Fallzahlen, die im dort verwendeten Maßstab in der Breite der Linie komplett untergehen. Wie lange werden sich die derzeitigen Einschnitte durchalten lassen? Die Konkurse und Massenentlassungen häufen sich jetzt schon, die irrationalen Panikhandlungen ebenfalls. Wann wird dieses strenge Regime am allgemeinen Widerstand zusammenbrechen? Meine derzeitige Schätzung besagt, daß dies genau zur Unzeit passiert und genau die Spitze der Welle noch höher und steiler machen wird, als sie es ganz ohne Eingriff gewesen wäre. Diese Spitze trifft dann auf eine zusammengebrochene Wirtschaft und Infrastruktur. Die Krankenhäuser könnten im schlimmsten Fall ohne Strom, Wasser und Lieferketten dastehen. All das ist unnötig und durch falsche Maßnahmen künstlich erzeugt. Was jetzt notwendig wäre, ist die Wirtschaft und das Gesellschaftsleben so zu stützen und zu stabilisieren, daß sie der Belastungsprobe, wenn sie dann in einem Monat kommt, standhalten können.
Das unten folgende ist inzwischen falsch und überholt. Der wirkliche Kölner Verlauf steht täglich aktualisiert auf Covid-Koeln.htm. Fraglich bleibt allerdings, ob kurzfristige Soforteffekte einen Einfluß auf den oben und an vielen anderen Stellen prognostizierten und aller Erfahrung entsprechenden mittelfristigen Verlauf haben.
Ergänzung noch am Abend des 2020-03-19
Wie sollte es auch anders sein? Bei nur 600 erkannten Fällen in einer Millionenstadt – wer soll da in der Öffentlichkeit denn wen anstecken? Anders ist es wie oben gezeigt am Beginn der echten Welle, aber jetzt?
|
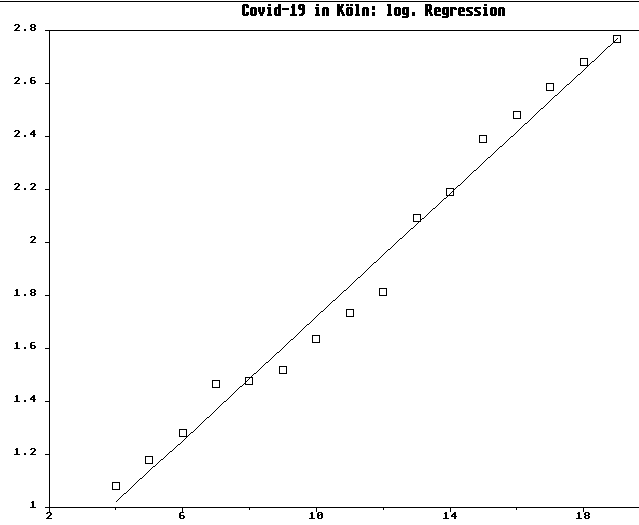
| Abb. 4: Dekadischer Logarithmus der für Köln täglich gemeldeten Fallzahlen im Vergleich zur idealen Regressionsgerade. |
Die vom Kölner Stadt-Anzeiger 
täglich gemeldeten Fallzahlen folgen, bis auf einzelne offenbar der Meldepraxis geschuldete Sprünge, fast exakt der idealen Regressionsgerade für einen exponentiellen Verlauf. Es ist keinerlei Einfluß irgendeiner der äußerst restriktiven Maßnahmen erkennbar. Genau das entspricht exakt der Erwartung und belegt, wie sinnlos und schädlich sie zum aktuellen Zeitpunkt sind.
Welche Chance haben wir, daß diese Eingriffe dann, wenn sie sinnvoll und notwendig sein werden, noch greifen können und durchsetzbar sein werden?
Zum Anfang Übersicht Kommentare Home & Impressum
Roy M. Anderson, Hans Heesterbeek, Don Klinkenberg & T. Déirdre Hollingsworth, How will country-based mitigation measures influence the course of the COVID-19 epidemic? The Lancet (2020), preprint, 1–4. <DOI:10.1016/S0140-6736(20)30567-5>.
Lancet2020.03-Supplement1.pdf, Lancet2020.03-Supplement2.pdf, Lancet2020.03-Supplement3.pdf
There are diicult decisions ahead for governments. How individuals respond to advice on how best to prevent transmission will be as important as government actions, if not more important. Government communication strategies to keep the public informed of how best to avoid infection are vital, as is extra support to manage the economic downturn.
Rafael Mikolajczyk, Ralf Krumkamp, Reinhard Bornemann, Amena Ahmad, Markus Schwehm & Hans-Peter Duerr, Influenza, Einsichten aus mathematischer Modellierung. Deutsches Ärzteblatt 106 (2009), 777–782. <DOI:10.3238/arztebl.2009.0777>.
Hintergrund: Beim Auftreten von ersten Fällen einer neuen Infektionskrankheit stellt sich die Frage nach dem weiteren Verlauf der Epidemie und nach angemessenen Interventionsmaßnahmen zum Individual- und Bevölkerungsschutz. Mathematische Modelle liefern einen wichtigen Beitrag zur Beantwortung dieser Fragen. In diesem Beitrag beschreiben die Autoren die Grundkonzepte der mathematischen Modellierung von Infektionskrankheiten, illustrieren diese an einem einfachen Beispiel and stellen Ergebnisse von Modellierungsarbeiten zu Influenza vor.
Methode: Darstellung der mathematischen Modellierung von Infektionskrankheiten und selektives Literaturreview.
Ergebnisse: Grundkonzepte der mathematischen Modellierung von Infektionskrankheiten – Basisreproduktionszahl und Generationszeit – erlauben es, den Verlauf einer Epidemie besser zu verstehen. Modellierungsstudien auf der Basis von früheren Influenzaepidemien suggerieren, dass am Anfang der Epidemie, sofern keine Impfung zur Verfügung steht, die Isolierung von Erkrankten und die medikamentöse Prophylaxe bei Personen, die einen Kontakt mit der Krankheit hatten, den Anstieg der epidemischen Kurve verzögern kann. Im weiteren Verlauf der Epidemie können Einschränkungen der Kontaktzahlen (zum Beispiel Schulschließungen) eine wirksame Intervention darstellen, um den Verlauf der Epidemie abzumildern. Die Abmilderung des Epidemieverlaufs wirkt sich jedoch nur gering auf die Gesamtzahl der betroffenen Personen aus.
Schlussfolgerungen: Die mathematische Modellierung ist ein wichtiges Werkzeug für das Verständnis des epidemischen Geschehens und für den Vergleich und die Planung von Interventionen.
Keywords: Influenza | Epidemie | Krankheitsverlauf | Infektionsabwehr | Prävention